Меню сайта


Эконометрика

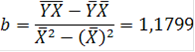
3) Оценим тесноту связи с помощью показателей корреляции и детерминации:

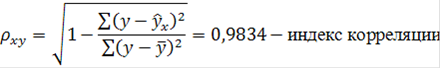
По шкале Чаддока индекс корреляции показывает весьма высокую тесноту связи.

) Оценим с помощью средней ошибки аппроксимации качество уравнений:

В данном случае . Можно говорить что полученное уравнение регрессии весьма точно.

) Найдём коэффициент эластичности:

корреляция регрессия детерминация прогноз

В случае степенной функции коэффициент эластичности выглядит так:

При изменении факторов на 1% результат в среднем изменится на 1,1799%

) Оценим с помощью критерия Фишера (F) статистическую надежность модели:

Критерий Фишера можно определить по формуле:

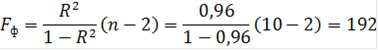
Отсюда можно сделать вывод, что уравнение регрессии статистически значимо и надёжно.

Гиперболическая регрессия

№ п/п

x

y

1

165

12,6

0,006061

0,000037

0,076364

12,2

0,4

0,16

3,82

14,59

3,17

2

125

9,4

0,008

0,000064

0,0752

10,4

-1

1

0,62

0,39

10,24

3

115

9,3

0,008696

0,000076

0,080869

9,7

-0,4

0,16

0,52

0,27

4,30

4

85

6,2

0,011765

0,000138

0,072941

6,9

-0,7

0,49

-2,58

6,66

11,29

5

95

7,6

0,010526

0,000111

0,08

8,0

-0,4

0,16

-1,18

1,39

5,26

6

135

11,7

0,007407

0,000055

0,086667

10,9

0,8

0,64

2,92

8,53

6,84

7

155

13,2

0,006452

0,000042

0,085161

11,8

1,4

1,96

4,42

19,54

10,60

8

75

5,3

0,013333

0,000178

0,070667

5,4

-0,1

0,01

-3,48

12,11

1,89

9

105

8,0

0,009524

0,000091

0,076190

8,9

-0,9

0,81

-0,78

0,61

11,25

10

65

4,5

0,015385

0,000273

0,069231

3,5

1

1

-4,28

18,32

22,22

∑

1120

87,8

0,097149

0,001029

0,773291

 

0.1

6,23

0

82,41

87,06

Ср.зн.

112

8,78

0,009715

0,000103

0,077329

 

0,01

0,623

0

8,241

8,706

Перейти на страницу: 1 2 3 4 5