Однофакторный регрессионно-корреляционный исследование экономической модели

ta2 4,1369 > tта6л = 2,1

то отвергаем гипотезу о незначимости коэффициентов уравнения регрессии а1 и а2.

. Влияние факторов на зависимую переменную

Проанализируем влияние включенных в модель факторов на зависимую переменную по модели. Учитывая, что коэффициенты регрессии невозможно использовать для непосредственной оценки влияния факторов на зависимую переменную из-за различия единиц измерения, вычислим соответствующие коэффициенты эластичности, β - коэффициенты:

,

,

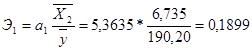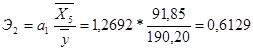Таким образом, при увеличении расходов на рекламу на 1 % величина объема реализации изменится приблизительно на 0,2 %, при увеличении потребительских расходов на 1 % величина объема реализации изменится на 0,61 %.

Кроме того, при увеличении затрат на рекламу на 4,0053 ед. объем реализации увеличится на 22 тыс. руб. (0,5755*37,3291 ≈ 22), при увеличении потребительских расходов на 15,1568 ед. объем реализации увеличится на 19 ед. (0,5153*37,3291 ≈ 19).

. Точечное и интервальное прогнозирование

Найдем точечные и интервальные прогнозные оценки объема реализации на два квартала вперед.

Для построения прогноза результативного признака Y и оценок прогноза необходимо определить прогнозные значения, включенных в модель факторов Х2 и Х5. Построим линию тренда для временного ряда «Индекс потребительских расходов» (рис. 10).

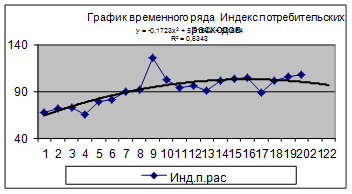
Рис.10. Результат построения тренда и прогнозирования по тренду для временного ряда «Индекс потребительских расходов»

В качестве аппроксимирующей функции выбран полином второй степени - парабола:

Х5 = 58,664+5,5154t - 0,1723t2

по которой построен прогноз на два шага вперед, причем прогнозные значения на 21-ый и 22-ой периоды соответственно составляют:

Х5(21) = 58,664 + 5,5154*21 - 0,1723*212 =98,5031,

Х5(22) = 58,664 + 5,5154*22 - 0,1723*222 =96,6096.

Построим линию тренда для временного ряда «Затраты на рекламу» (рис. 11).

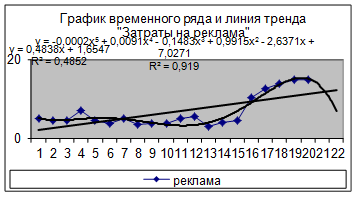
Рис.11. Результат построения тренда и прогнозирования по тренду для временного ряда «Затраты на рекламу»

Для фактора Х2 «реклама» выбираем полиномиальную модель пятой степени (этой модели соответствует наибольшее значение коэффициента детерминации):

Х2 = -0,0002*t5+0,0091*t4-0,148*t3+0,991*t2-2,6371*t+7,0271.

Полиномы высоких порядков редко используются при прогнозировании экономических показателей. В этом случае при вычислении прогнозных оценок коэффициентов модели необходимо учитывать большое число знаков после запятой.

Прогнозные значения на 21-ый и 22-ой периоды соответственно составляют:

Х2(21= -0,0002*215+0,0091*214-0,148*213+0,991*212-2,6371*21+7,0271=-28,9921,

Х2(22)= = -0,0002*225+0,0091*224-0,148*223+0,991*222-2,6371*22+7,0271=-46,2459

Для получения прогнозных оценок переменной Y по модели

подставим в неё найденные прогнозные значения факторов X2 и X5, получим

Ŷ(21)

Ŷ(22)

Доверительный интервал прогноза имеет границы:

верхняя граница прогноза: Ŷ(n+1)+U(l),

нижняя граница прогноза: Ŷ(n+1)-U(l),

где , .

Имеем

,
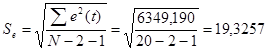