Однофакторный регрессионно-корреляционный исследование экономической модели

Построим линейное уравнение парной регрессии Y по X. Используя данные таблицы 3, имеем:

,

.

Получим линейное уравнение регрессии:

Y = 4,51276+0,008392* х (4)

Тесноту полученной линейной модели характеризует линейный коэффициент парной корреляции:

rxY = β *

Коэффициент детерминации при этом равен:

R2 = r2xy = 0,853822 = 0,7290

Это означает, что 73% вариации фактора Y объясняется вариацией фактора х. Средняя ошибка линейной аппроксимации составляет:

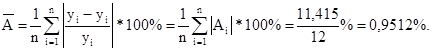
Проведя потенцирование уравнения (4), получим искомую нелинейную (показательную) модель

y =91,1733*1,00843x (5)

Результаты вычисления параметров показательной кривой (1) можно проверить с помощью ППП Excel, для чего используем встроенную статистическую функцию ЛГРФПРИБЛ. Порядок вычисления аналогичен применению функции ЛИНЕЙН.

Результат вычисления функции ЛГРФПРИБ представлен на рисунке 4:

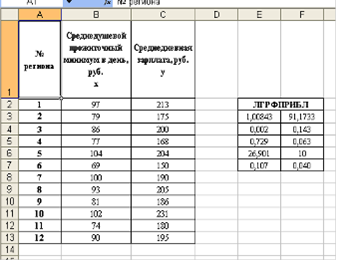
Рис. 4. Результат вычисления функции ЛГРФПРИБЛ

Для расчёта индекса корреляции ρxy нелинейной регрессии воспользуемся вспомогательной таблицей 4.

Таблица 4