Однофакторный регрессионно-корреляционный исследование экономической модели

а. Построим линейное уравнение парной регрессии y по x. Используя данные таблицы 2, имеем

β = =

α = y - β * x = 191,417-1,570*87,667=53,809

Тогда линейное уравнение парной регрессии имеет вид:

y = 53,809+1,570 * x.

Оно показывает, что с увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная зарплата возрастает в среднем на 1,570 руб. 2б. Учитывая:

σx = 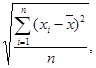σy =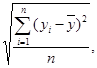

оценим тесноту линейной связи с помощью линейного коэффициента парной корреляции:

rxy = β *

Найдём коэффициент детерминации:

R2 = r2xy = 0,7246

Это означает, что 72% вариации заработной платы y объясняется вариацией фактора х - среднедушевого прожиточного минимума.

в. Для оценки качества полученной модели найдём среднюю ошибку аппроксимации:

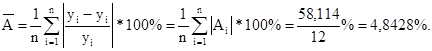
В среднем, расчётные значения отклоняются от фактических на 4,8428%. Качество построенной модели оценивается как хорошее, т.к. значение - менее 8%.

г. Для оценки силы связи признаков y и х найдём средний коэффициент эластичности:

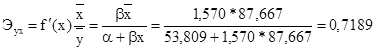
Таким образом, в среднем на 0,72% по совокупности изменится среднедневная зарплата от своей средней величины при изменении среднедушевого прожиточного минимума в день одного трудоспособного на 1%. Бета-коэффициент:

β yx = β *

показывает, что среднее квадратическое отклонение среднедневной зарплаты изменится в среднем на 85% от своего значения при изменении прожиточного минимума в день одного трудоспособного на величину его квадратического отклонения.

д. Для оценки статистической надёжности результатов используем F - критерий Фишера.

Выдвигаем нулевую гипотезу Но о статистической незначимости полученного линейного уравнения.

Рассчитаем фактическое значение F - критерия при заданном уровне значимости γ = 0,05

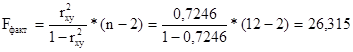
Сравнивая табличное Fтабл = 4,96 и фактическое Fфакт = 26,315 значения, отмечаем, что Fтабл < Fфакт ,

что указывает на необходимость отвергнуть выдвинутую гипотезу Но.

2е. Оценку статистической значимости параметров регрессии проведём с помощью t- статистики Стьюдента и путём расчёта доверительного интервала для каждого из показателей.

Выдвигаем гипотезу Но о статистически незначимом отличии показателей регрессии от нуля: α = β = rxy = 0.

Табличное значение t- статистики tтабл для степеней свободы

при заданном уровне значимости γ = 0,10 составляет 1,8.

Определим величину случайных ошибок:

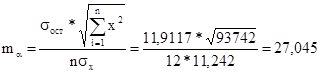
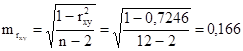
Найдём соответствующие фактические значения t-критерия Стьюдента:

,

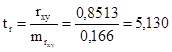
Фактические значения t - статистики превосходят табличное значение tтабл = 1,8

tβ = 5,130 > tтабл , tα = 1,990 > tтабл , tr = 5,130 > tтабл

поэтому гипотеза Но о статистически незначимом отличии показателей регрессии от нуля отклоняется, т.е. параметры α, β, rxy не случайно отличаются от нуля, а статистически значимы.