Однофакторный регрессионно-корреляционный исследование экономической модели

Для расчёта доверительных интервалов для параметров α и β определим их предельные ошибки

,

.

Доверительные интервалы

для параметры a: (5,128; 102,490)

для параметры β: (1,019; 2,120)

С вероятностью

r = 1 - γ = 1 - 0,05 = 0,95

можно утверждать, что параметр β, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.

3. Проверим результаты, поученные в пункте 2 с помощью ППП Excel.

Параметры парной регрессии вида y=a+bx определяет встроенная статистическая функция ЛИНЕЙН. Результат вычисления функции ЛИНЕЙН представлен на рисунке 2:

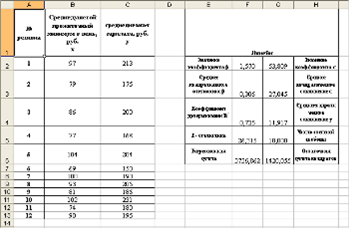
Рис. 2. Результат вычисления функции ЛИНЕЙН

С помощью инструмента анализа данных Регрессия, помимо результатов регрессионной статистики, дисперсионного анализа и доверительных интервалов можно получить остатки и графики подбора линии регрессии, остатков и номинальной вероятности.

Результаты регрессионного анализа для данных задачи представлены на рисунке 3.

регресионный корреляция детерминация

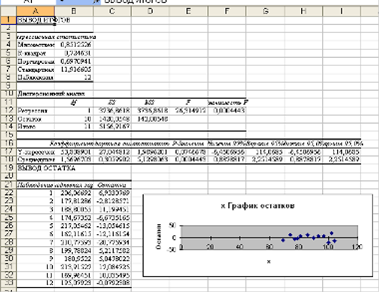
Рис. 3. Результаты применения инструмента Регрессия

Сравнивая полученные вручную и с помощью ППП Excel данные, убеждаемся в правильности выполненных действий.

. Построению показательной модели

(1)

предшествует процедура линеаризации переменных.

Прологарифмируем обе части уравнения (1), получим:

ln y = ln α + x * ln β (2)

ведём обозначения

Y = ln y, C = ln α , B = ln β

Тогда уравнение (2) запишется в виде:

Y = C + B * x. (3)

Параметры полученной линейной модели (3) рассчитываем аналогично тому, как это было сделано ранее. Используем данные расчётной таблицы 3.

Таблица 3